Ch 6. Measuring Generalizing Intelligence
This chapter introduces a test and quantitative measure for generalizing intelligence in artificial intelligence implementations. This is unique, in that it specifically discriminates a generalizing capacity from mere effectiveness in one or more domains. Insights are made into the structure of knowledge relationships, along with the concept of anti-effectiveness, which reveals the unavoidable problem of constructed systems being susceptible to delusion as a foundational issue, as distinguished from concerns about what constitutes the proper choice or way to deliver values and knowledge. Finally, an epistemic hierarchy is uncovered that is the result of order inducing structures between domains of knowledge and effectiveness. These results advance the state of the art in artificial intelligence by providing an absolute test for generalizing intelligence.
6.1 Purpose and Applications
Current tests and measures of artificial intelligence have built-in assumptions about anthropomorphism, agency, and interaction with the environment [1, 2, 3, 4, 5]. The modern artificial intelligence literature, at the time of this writing, suggests the use of “universal” tests of intelligence in a given domain by optimizing an idealized agent over an environment [6, 7, 8, 9, 10]. The problems with these tests are many, including, but not excluding:
The inability to be computed or appreciably estimated in practice due to reliance on pure mathematics and/or abstract notions. This results in an impractical test that, while interesting, provides neither insight into the nature of intelligence nor how these systems might function in practice.
Built-in assumptions about “agents”, including the assumption that the entity has to be regarded, abstracted, or treated as an agent, which also, unfortunately, carries the confusion of ascribing agency, volition, and goals to something which would otherwise be incapable of such functionality.
Built-in assumptions about utility functions, which have been interpreted in extreme scenarios, [11, 12] which do not reflect the reality of such systems. This has created a misguided direction of research that emphasizes AI safety through the loading, specification, or design of utility functions [13].
Lacks a generalizing intelligence test, despite the label “universal”. This represents a fundamental problem, as it can be defeated by the machine learning problem.
Utility functions, agents, and agency have plagued the analysis of effective systems since these notions were applied to artificial intelligence. Law and policy makers require a definition that discriminates between generalizing and non-generalizing intelligence. It is not sufficient to simply entail a series of goals for an abstract “agent.”
Definition. Machine Learning Problem. Suppose there is a machine learning system that is configured so that it can be directed to learn new domains without being reprogrammed or reconfigured. To do this, it is constructed in such a way that each of its domain-specific knowledge representations are separate but jointly accessible to the entirety of the system. It meets the intuitive notion of general purpose learning, despite lacking the generalizing capacity that enables knowledge-transfer between domains.
The test of generalizing intelligence in this chapter was designed to address the machine learning problem. It is designed to detect the direction and magnitude of the transfer of knowledge between domains.
Generalizing intelligence is more than the ability to learn many domains. It is about the application of previous effectiveness to increase effectiveness in new ones, above and beyond what would have been demonstrated if learned in isolation. Current universal tests of intelligence are fundamentally incapable of detecting this, and have no sensitivity to knowledge transfer, as it is just implied in the overall performance.
Knowledge transfer has to be explicitly measured, as the application of cross-domain knowledge is fundamental to generalizing intellectual capacity. It entails all of the traits we would typically ascribe to generalizing capacity, including abstraction, analysis, and synthesis, along with analogizing. These are built-in to the notion of generalizing intelligence as fundamentally as universal intelligence tests have included agency and utility functions. Unfortunately, for the great work done in these areas, there is no way to fix them without a total rewrite of their basis; the tests are built on philosophies that can not account for the structure of knowledge relationships. As such, a completely new measure and experimental apparatus must be devised.
What is to be introduced involves new terminology and straightforward mathematics. An experimental setup is described such that one can acquire the data in the correct way and subsequently use it to test for the presence of generalizing intelligence in any system which can be properly isolated, as per the setup. These results are quantitative and have been normalized to a simple scale that can be informative with as little as two domains and a single participant. It can be used in isolation or as a comparative measure between test participants in one or more domains. Once the final value is computed, it can also be utilized in a domain-independent manner that can quickly discriminate generalizing capacity. This can lead to novel algorithms that can be directed to search for and improve upon existing implementations.
6.2 Effective Intelligence (EI)
Several prerequisite measures are required before generalizing intelligence can be calculated. The first of these is effective intelligence, or EI, for short.
Definition: Effective Intelligence. An absolute performance measure based on the steps and time taken by the participant. It is based on the least amount of actions in the least amount of time that are physically possible for the domain, under the condition that consistent success is always upheld.
Any measure can be used so long as it remains on the interval (0, 1] and follows some conceptual qualifications. A value of 1 indicates maximum possible effectiveness. Zero is excluded, as it indicates a failure to demonstrate the condition of consistent success; all of the dependent calculations for the generalizing intelligence test necessitate this condition. This concept will be discussed in more detail ahead, after domains of effectiveness have been introduced.
Definition: Domain. An area, task, or process in which a subject can demonstrate intelligence.
The notion of a domain is essential to both the proper construction of the experiment and to the rest of the analysis. The more narrowly tailored it is, the more informative it becomes. Further, one must take into account the machine learning problem when choosing an appropriate measure of the effectiveness in the domain. This weighs on the final calculation in the tests of effectiveness, as one must eliminate undue influence in the application of prior knowledge to new domains. This is why it is strongly recommended that EI be used instead of simple accuracy or quality assessments.
The EI measure has been specifically devised as a basis for the next stages of the test. It automatically culls assumptions, and forces the participant and domain to conform to the epistemological standards in an objective manner. This helps to avoid a qualitative analysis, as the epistemological constraints are built directly into EI and can not be accidentally bypassed.
While a total percentage of accuracy in a large number of test cases is informative, it can lead to issues with the machine learning problem, which confuses domains with data. For example, facial recognition of humans against certain mammals may produce partial successes due to structural similarities and symmetries, leading to a distortion of the general intelligence testing. To eliminate this, effective intelligence is not concerned with how accurate or how much quality the participant has demonstrated in its domain, but rather, how efficient it was in doing it. This has to be done, as it is the only objective terms available across all possible domains.
The basis for EI is thus the number of actions and the amount of time it took to be successful. This is a potentially difficult notion to unpack, as it necessarily places constraints on test perspectives. However, this apparent simplification belies a powerful feature; its purpose is to keep the analysis objective, regardless of the type of domain or participant involved. The easiest way to do this is to factor out subjectivity. EI does this by making a high standard of quality implicit to the measure. In this way, virtually any subjective domain can be made objective. This is its benefit over other requisite measures that could be chosen.
By contrast, leaving quality built into a measure forces one to place numbers on subjective figures. This does not obtain objectivity. Only when the qualitative aspect is factored out can EI be used in its proper sense. This is why it is included in the definition as the consistent success principle.
While consistent success is open to interpretation, it should be appreciably high, and must be applied the same way across all domains and participants in any treatment of these tests. In some domains, it should disqualify the subject from being considered as having effectiveness at all, and, as a result, remove it from consideration under that domain; it is not important how effective a participant is some of the time if the domain is so vital that anything less than consistent success is demanded. This ensures that the consistent success principle has a high standard of quality.
Consider golf as an example of a domain that exemplifies the distinction between EI and other measures of effectiveness. The objective of golf matches one half of the definition of effective intelligence exactly: minimize the number of strokes to obtain the best score. The least number of strokes is the number of holes played, assuming the ability to get a hole-in-one at each attempt. This, of course, may seem an impossible scenario, but it accurately represents the notion of perfect effectiveness. Time is not considered in golf for reasonable participants, so, as such, it has a best time that is fixed at 1, and is thus factored out of the assessment automatically.
This same situation is applied to more complex scenarios, such as the finite description of the implementation of an artificial intelligence. This concerns not only the length of the description but the total cost in cycles or running time. It may be appropriate, in some cases, to conduct all tests on the same hardware, and only account for time or actions alone. The equations are flexible enough to support this: simply set all actions or time to 1, as was done in the golf example above.
The effective intelligence (EI) of some participant for domain A is:
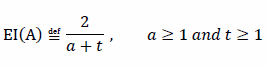
Where a is the number of actions and t is the amount of time taken to arrive at consistent success in domain A. This has a number of important observations. Namely, the dimension of actions and time are flexible. They can be factored in or out by only considering either actions or time, or they can be combined to have both. In all cases, the appropriate relative and absolute scales for performance in EI will reflect it correctly. Note, for brevity in the definition, the participant is assumed as a constant and not made an explicit argument of EI; this convention is a useful simplification, as there is never a direct comparison between participants in any of the mathematical definitions.
The most important aspect of EI is that it provides an absolute measure of effectiveness in the domain, both alone and when comparing change between observations within the same domain. In each case, the percentages will agree in proportion to changes in either time or action steps.
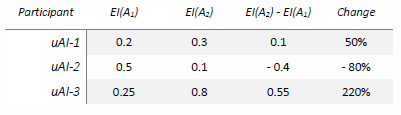
To help illustrate comparisons, the following simulated data is provided for three AI implementations over a single domain, with two observations each:
What the table indicates is that uAI-1 and uAI-3 became more effective, with uAI-3 becoming the most effective. Notably, uAI-2 decreased in effectiveness by a significant factor. Naturally, a full sampling of these results would be indicated over hundreds or thousands of tests to find a mean value of EI that was stable. These percentages in change could also be compared against other subjects in the test, giving a comparison of how effective they are in relation to the most effective implementation, uAI-3.
This prepares us for the notion of measuring self-modification and improvement. That is to say, if we were to consider the data tables as being different versions of the same artificial intelligence, then this would reflect a single-domain self-improvement. Indeed, that is one of the benefits of utilizing this measure, as it works between subjects just as well as it does for different versions of itself.
Again, these tests are not a qualitative assessment, such as how much “better” it became at detecting something, but rather, how much more effective it became at doing more of the things that constitute the domain. The assumption of quality has already been provided by the condition of consistent successes, which, for a subjective domain, such as creating music or art, could have been that reasonable people would not have been able to tell that it was not done by a human expert. What EI indicates is an objective ability to do it more efficiently, and in less time.
Before one attempts to criticize the notion of efficiency that underwrites effectiveness, consider the fact that the only thing that allows many encryption algorithms to be effective is that it is unreasonably difficult, in terms of time and actions, to break them through a brute-force attack [14, 15, 16]. More to the point, it is commonly believed that strong AI will require significant computational resources. This is a very mistaken belief.
The risk here is that the application and use of strong artificial intelligence, including the hardware that allows it to operate, will be much broader than anticipated. This would shatter the threat and security models, leaving us completely unprepared when the public begins using it. The belief that strong artificial intelligence will require large resources is a threat all unto itself. This relates back to the defense of EI as a measure, as this threat is merely a change in the effectiveness of the implementation. In other words, undervaluing efficiency is the same as overestimating the computational demands of this technology.
This risk has been worsened by the popularity of biologically inspired designs in artificial intelligence research. This is especially damaging for AI security, as it is very likely that non-biological algorithms will be orders of magnitude faster than their biologically inspired counterparts.
Many problems are, indeed, a matter of how quickly it can be done, and in how few steps. This is especially true for labor tasks in which a robot equipped with strong artificial intelligence would need to operate. It could range from obstacle avoidance to surgery; the case for maintaining the same quality, while minimizing time and actions, is the very essence of perfection for a wide range of tasks.
There is an economic impact of great significance attached to high effective intelligence, even for what one would consider purely qualitative domains. If both a human and a strong AI implementation were able to make quality products, the most effective worker would be the one who could do so in the least time and steps. If all of this can be done in a thousand times more volume than a human, with the same or greater quality, it necessarily obsoletes that human in the domain.
Care must be taken to ensure that the principle of consistent success is never undermined. When speaking of the effective intelligence of a process, it should be automatically understood that it has demonstrated the qualitative aspects that are expected of the domain. It does not make sense to discuss efficiency where quality is lacking. The other side of this argument is that quality must not be minimized.
It is not acceptable to take the condition of consistent success as a backward argument for minimizing quality, especially in an effort to lower the acceptable barriers of entry. This would be akin to cheap manufacturing with known defects or marginal quality. The spirit of the consistent success principle is to maximize quality by setting a high standard for the domain. Then, and only then, can quality be factored out.
As an ethical requirement, any experiment or process which utilizes the measures from this chapter must include a statement on the quality standards, including all data and tests that were used to assure that the participant was qualified for inclusion. Further, this must be done for each and every domain in the ensemble.
Effective intelligence can also provide insight into learning over time by sampling a subject at various intervals in the adaptation process. For example, consider Figure 6.1, which has been scaled and made precise from simulated data. The gray line represents EI sampled at various points. The curves are smoothed and interpolated from several data points. The x-axis represents the sample space for some interval of time, with the y-axis being the magnitude or value. S-curves in effective intelligence are anticipated for the majority of participants. Adaptation is the 1st derivative of effectiveness and represents the rate of learning at that particular point in time. It is expected to grow and then decline, but remain positive or zero. Acceleration is the 2nd derivative of effectiveness and determines the rate at which it is changing in adaptation.

High acceleration and adaptation should be indicated for strong AI participants. Notably, the effectiveness will tend to level off. These charts can be useful in determining when an implementation is no longer making any appreciable gains, or in comparing how different versions adapt to the domain. Even if high EI is achieved, it is always better to get there faster, and with only a single drop in adaptation. This could be considered a kind of reflexive EI, and should be included as part of the analysis of single-domain intelligence.
6.3 Conditional Effectiveness (CE)
In order to perform the calculations for generalizing intelligence, a second requisite measure must be calculated from the EI. This will be used to create an arrangement of data that will become the conditional effectiveness of the domain ensemble for each participant. As with EI, this will also be referred to as just CE.
This stage is the most intricate part of the calculation, as it requires a test configuration that must not deviate in experimental control. The data is tabulated, with the end result being a modified adjacency matrix [17, 18, 19].
Conditional effectiveness has a notion of directionality. The magnitude of this directionality is a measure of the closeness between two domains, and is related to the order in which they were learned. This is difficult, as it depends both on the domains and the participant. Not all participants are going to be able to close the distance between domains.
It is said that a domain is conditionally effective because it is contingent upon having demonstrated an improved effectiveness as a direct result of having previous effectiveness in a different domain. As such, CE is a correlation of improvement between domains. This is the critical data that will be required to detect and measure generalizing intelligence.
The first step in understanding conditional effectiveness is to know that all individual runs of the experiment must be isolated:
Definition: Isolated Domain. A participant that has become effective at a domain with no prior information provided to or within the system.
Isolated domains must exclude moral subjects from experimentation, as it necessitates wiping the memory or knowledge stored in the implementation in order to create unbiased measurements. It may be possible, with significant statistical effort and experimental reconfiguration, to adapt the experiment to work without truly isolated domains, but the results will never be as accurate. As was mentioned in the Machine Consciousness chapter, it may be possible to construct strong AI implementations that do not have personhood or agency in the sense that would qualify as moral subjects. In such cases, it may be permissible, although not without serious consideration beforehand, to perform this experiment.
Naturally, in the developmental stages of strong AI, one is already meddling in the deep ethical gray; better to know it is capable of generalizing intelligence sooner rather than later. It is also remotely possible that an implementation will be able to exhibit generalizing intelligence without being sentient, thereby bypassing the moral subject consideration entirely. However, if the new strong AI hypothesis is true, then sentience is a minimum requirement for achieving generalizing capacity. This possibility induces a moral obligation on the experimenter to consider the ramifications of the isolating procedure.
The reason for the isolated domain is due to the previously mentioned machine learning problem. Overcoming this demands absolute experimental control in order to eliminate its influence over the data. A general learner is possible with current narrow AI algorithms, but this does not mean that it applies effectiveness across domains. In other words, general learning does not imply general intelligence. To test this, we must isolate domains and measure their effectiveness, both alone and in juxtaposition. This is the only way to determine the various combinations.
Each sampling of the total effectiveness must be conducted to a high degree of confidence. Statistical methods must be used to prepare the expected EI to account for variance and biases. This should be a basic part of the data preparation process. The implementation of the participant must then be reset for each domain, and the process repeated for each permutation. The procedure is as follows:
Isolate or start from ex nihilo implementation.
Measure
EI(A).Isolate.
Measure
EI(B).Isolate.
Measure
EI(A|B)by learning ‘B’ then takingEI(A)again.Isolate.
Repeat in opposite learning order.
Repeat for remaining domains in the ensemble until all permutations exhausted.
Conditional effectiveness is built on ordered effective domain pairs. The resulting total number of tests is thus the square of the number of domains minus the number of domains. This accounts for the fact that CE is 0 for a domain with itself. The CE is [-1, 1] with negative indicating a notion that will be referred to as anti-effectiveness.
Anti-effectiveness has not been experimentally observed, and is simply predicted by the mathematics of this test. It is an anticipated result of future generalizing intelligence algorithms that exploit the directionality between domain pairs. An entire section will discuss anti-effectiveness after this section, so it will be set aside for now.
It should be noted that conditional effectiveness is signed, with any deviation from zero, positive or negative, indicating a transfer between domain pairs. This last is crucial, as it comes into play in the final calculation for generalizing intelligence. While the sign of CE is ultimately irrelevant for determining generalizing intelligence, it is useful where anti-effectiveness is an expected and desirable outcome.
The conditional effectiveness (CE) of some participant for domain ‘A’, given domain ‘B’ is:

EI(A|B) is measuring the EI for domain A only having previously had the participant learn domain B, with all measurements done in isolation.
The CE is an absolute measure of the improvement of effectiveness having previously demonstrated effectiveness in another domain. It is built on the detection of the sign internally due to the need to handle the distance from zero and one, respectively, and the special case that values around zero are usually indicating a zero CE unless perfect consistency is previously established to a high degree of confidence in the expected EI for each domain. That is why almost equal to zero is used rather than exactly equal to zero. In all cases, a properly scaled measure of absolute improvement is provided, whether it is the distance to zero or the distance to one. It was created this way to ensure that the percentage interpretation of the CE is correct regardless of the sign, despite the difference in the distances for increased or decreased effectiveness. This allowed for reflection of the metric to accommodate the anti-effectiveness notion. The CE is ultimately restricted to [-1, 1] and can be interpreted as a percent improvement, with -1 or 1 being a perfect improvement.
The failure to detect CE does not necessarily mean that the participant lacks generalizing intelligence. It could be that the domains are unrelated, and that no participant could have been expected to improve as a result. These are called exclusive domains. By contrast, mutual domains have the potential of benefiting from cross-domain knowledge transfer. Note that this is not just a function of the artificial intelligence, but must be present within the structure of the domains. Mutual domains need not be directly related in subject matter to be exploited by generalizing intelligence.
It must also be pointed out that the notion of a domain does not need to be broad. It can and should be very specific. For example, the domain B could be a tutorial on how to do domain A better. If the tutorial was reasonable, and the domains were mutual, it would be expected that there should be a positive CE for implementations with sufficient generalizing capacity. This is the advantage of factoring out subjectivity and quality assessments. The EI for the tutorial in domain B would have simply been the performance of how quickly it adapted to the knowledge, and, upon the condition of consistent success, that it accurately reflected the improvement it in its knowledge representation each time. This, however, is only one example out of an infinite number of situations and domains.
In graph theory, an adjacency matrix is a square matrix representing the connectivity of the vertices of the graph. In this case, the matrix is asymmetric because the graph is directed. There are no self-loops in CE based graphs because, in these calculations, a domain can not be contingent upon itself. This results in zeros down the diagonal of the matrix. Normally, in an adjacency matrix, it is either just a 1 or a 0 depending on whether or not an edge is connected. In the CE matrix, however, this notion is extended to be a measure of how well connected they are, with -1 and 1 being the maximum in either direction.
The graph data is as follows: vertices represent domains and the edges are encoded in row-major order. This means that CE(A|B) would be the element at the first row and second column, and CE(B|A) would be the element at the second row and first column.
A simulated CE matrix follows for a hypothetical strong AI, with hyphens representing zero diagonal for ease of readability:
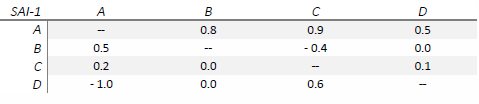
One possible graphical representation of the CE matrix is a clustered and stacked bar chart, as shown in Figure 6.2.
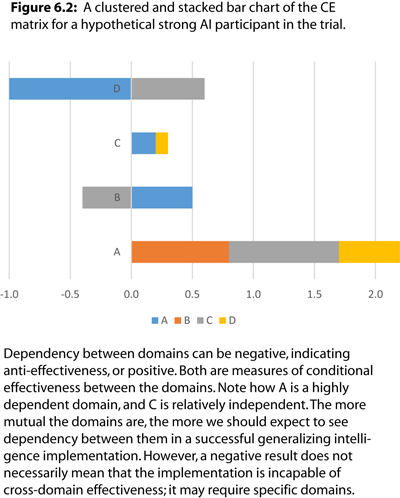
What this visualizes is that domain A is sensitive or dependent upon domains B, C, and D. Notice how none of the other domains exhibit CE with domain B, and how domain A is highly anti-effective for domain D. This sets up a potential knowledge hierarchy for the domains, and is a concept that will be discussed in more detail later.
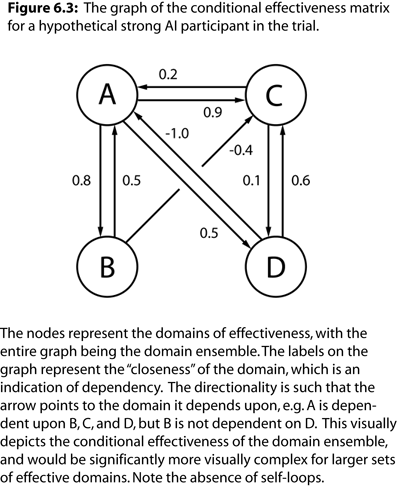
In general, the more domains in the ensemble, the more informative the CE matrix will become, and, in turn, the more informative the resulting general intelligence score. Many other analyses can be performed on the CE matrix that apply to networks or graph theoretic measures, especially those that utilize weighed assessments. However, we will only focus on the measure of the CE matrix itself, which is used to calculate the resulting general intelligence score.
6.4 Anti-effectiveness
It is possible for CE to be reflected. When it is negative, it indicates a percent measure of the maximum possible drop in effective intelligence as a result of the other domain being known beforehand. There was a mathematical formulation that clamped reflected values to zero, and hence made the resulting generalizing intelligence score easier to calculate, but the use of the reflected values was too important to leave out. As such, the definition for CE was made slightly more intricate to handle the proper scaling in either direction. This is noted here to document that other alternatives were considered.
What does anti-effectiveness indicate? That depends on whether or not it is a desirable result. First, in the desirable case, it is rather like an inoculation for knowledge. For example, if CE(A|B) is -0.5 then the participant becomes worse at A as a result of having known B. This might be considered a success in some circumstances, as it could be that domain A is of questionable moral or factual content, and now, as a result of having learned B first, it is less susceptible to influence from domain A. This dependency is also reliant upon the chosen metric for EI. The effectiveness variant would only indicate a slowdown in the efficiency, with zero still being informative, in that it indicates that it failed the test of consistent success. For other measures used in place of EI, however, anti-effectiveness could be even more informative.
While it is possible to achieve maximum anti-effectiveness, it may be impossible to attain its opposite, which would be a maximum positive CE. This is an important property, as anti-effectiveness is both desirable and non-desirable, depending on context.
Delusion on the part of the artificial intelligence is not a topic that is often discussed, but it raises some of the most significant security and safety concerns. Even with moderate self-security and various safeguards in place, what is to prevent effectiveness in domains based on delusion or false beliefs? This is connected to classic and modern problems in the philosophy of knowledge [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30].
The problem of delusion presupposes all of the security and safety in artificial intelligence, save for the integrity of the implementation itself. This is because, at some level, it must all collapse to a reliance upon the knowledge and information that makes up the foundation of the security for the system.
How do we know that the thing in question is isomorphic to the information necessary for its proper operation? Such information could be rules, programming, or the way it perceives and encodes the world, itself, and everything else. If that basis is intact but incorrect, it creates a problem altogether different from giving information, as it is not just a matter of specifying something if what it ultimately learns is never faithfully represented. This would cause a cascade of faults that would result in a breakdown of even the best security and safety mechanisms.
Each AI implementation will be a potential blank slate, and the way it represents and acquires knowledge will affect how well it demonstrates effectiveness between domains. Though, this potentially confuses effectiveness with the willingness to demonstrate what has been learned. It may simply be the case that such systems can still learn undesirable domains but never act on that knowledge. For example, being aware that someone is deluded in order to deal with them. However, one must not conflate anti-effectiveness with these higher-order constructs. It is a fundamental measure that detects how domains impact each other for a given learner, human or otherwise. This belies the impact that new domains have on existing knowledge.
Anti-effectiveness is thus a quantitative measure of delusion in circumstances where positive domain sensitivity is not the desired outcome. In this way, the enculturation of individuals can be seen as creating an epistemological hierarchy, one that spans everything from politics and religion to general knowledge. This is not a critique of one culture, but the very notion of culture itself, especially where it is a means of causing harm to others. Our collective inability to overcome delusion is indeed one of our greatest failings as a species. This absolutely must not be delivered upon our artificially constructed counterparts.
It is often believed that strong artificial intelligence automatically means “super intelligent”, or that one equals the other. That is not the case, as strong AI refers to the potential for generalizing intelligence, with actual capacity varying greatly between implementations. By contrast, a super-intelligent process is merely descriptive.
One can write a program to be super-intelligent at various narrow tasks, but if one is implying a maximal level of generalizing ability, that is altogether very different and specific. This is the essence that conditional effectiveness tries to capture.
To achieve maximum generalizing ability, one would have to exhibit the best possible CE in every case where such sensitivities were possible. Not all domains are mutual, and many will have no relation to each other, regardless of the intelligence or capacity of the participant.
All of this is said to point out that it is not automatic that an AI implementation will be able to discern truth from fiction, or that all knowledge is merely deducible from some prime order of facts that can be verified with just a little more calculation. Quite the opposite. The pursuit of truth is going to be filled with mistakes and approximations. It is not realistic to expect that a hypothetical best-case learning process will be able to discern, just as a matter of fact, that what it is becoming effective at is truthful, let alone morally correct. The latter is usually understood well enough, but the former is not. That is to say, being effective at delusional domains is much more insidious. Thus, it must not be assumed that intelligence implies the ability to navigate falsehood.
What anti-effectiveness truthfully replicates is the directionality of the effectiveness of learning domains, and this, in turn, induces an epistemic hierarchy. The hierarchy is absolute; CE only probes it out.
The ability for mutual domains to exist is something that is intrinsic to the structure of those domains, and the tasks and information they contain. It is not a product of the participant, human or otherwise. The ability to exploit those dependencies is literally the art of constructing effective strong artificial intelligence. It is the foundation of any possible generalizing intelligence, and what we will discover, if we eventually map it out, is that we can visualize knowledge in a massive weave of interdependencies, and that some domains will move to higher or lower prominence.
Indeed, one could envision a cladogram [31] or similar structure for thousands of domains of inquiry, representing a massive wheel of knowledge. Finding the optimal order in all of this could further speed up the learning process in artificial intelligence systems. This is well beyond the systematization of prerequisites, and is a gateway to computational epistemology [32, 33, 34, 35, 36, 37, 38, 39, 40].
There are instances of anti-effectiveness all around us in day-to-day human experience. What the mathematics indicate here is that these systems will be just as susceptible. Fortunately, we can at least measure CE and seek out the truth as a matter of guidance. In the cases where such processes are left to their own methods, however, it could result in deviation not just from our values but in the very dependencies that presuppose judgments on knowledge. This is why it is going to be vital that certain domains be considered mandatory prerequisites for any strong AI implementation, such as science, epistemology, and skepticism.
Though, care must be taken not to limit the future application of knowledge by imparting a single epistemological framework. For example, rationality alone could end up being dangerously misleading, as the only requirement to be rational is to be internally consistent; an internally consistent psychopathy is still harmful.
Note that this is separate from moral intelligence and the concept of value that is part of the interpreter in machine consciousness. That is to say, intrinsic values must exist to even allow moral processes to function, and, further, that simply having the ability to empathize is not enough to invoke an action, which is why there must be semantics in place to induce intrinsic values. However, anti-effectiveness hints at a complex interdependence, in that, if what is understood, perceived, or known is not representative of the facts, then it could betray any and all implementation semantics, including safeguards. Worse yet is that some of this could originate outside the implementation.
Another challenge with anti-effectiveness is that a positive CE is not always desired. This means that the sign of the CE measure is context dependent. It is not merely a matter of switching the learning order of the domains, as the relationship is not symmetric, but highly reliant upon the structure of the domains themselves.
Definition: Requisite Domain Ensemble. The learning of certain domains so as to give rise to the optimal course in the epistemic hierarchy, and to maximize or minimize anti-effectiveness, giving rise to the best possible tendency towards the correct representation of knowledge and information within the implementation that is practical.
Just as we have a basic education system in place for humans, an RDE should be provided to every strong AI implementation before it is deployed in the world. This should, at the very least, include scientific methodology, skepticism, and epistemology. This alone would eliminate a vast majority of problems.
Unfortunately, the RDE initiative will also cause political intrigue, as it selects a partition within the global graph of the epistemic hierarchy. Due to enculturation and bias, there will be those who will oppose such initiatives, as it will create anti-effectiveness in various religious, political, and ideological domains.
This is going to be a difficult time ahead, as early funding sources could subtly influence the knowledge relationships in widely distributed implementations of strong artificial intelligence. This is why the the RDE is so important to AI security. These subtleties will not be missed by those who will misuse them. Meanwhile, at the time of this writing, many AI researchers are either unaware or deny that concepts like the requisite domain ensemble even exist.
6.5 Generalizing Intelligence (G)
Generalizing intelligence will be referred to as G. The capital is used to distinguish it from a related measure in psychometrics called g-factor or general factor [41]. This notation is a nod to big O notation in computer science [42]. Unlike g-factor, G is an absolute and quantitative measure. It is calculated directly from the CE matrix.
G is on the interval [0, 1] with 1 being the absolute maximum that is possible. Values close to zero could potentially be considered non-existent, but should not be ignored, as the way in which G is calculated means that small values will dominate most CE matrices for participants exhibiting generalizing intelligence.
It is also vital that mutual and exclusive domains be understood. A negative indication of G does not mean that the participant lacks generalizing intelligence, but that it was (a) unable to display generalizing intelligence in that particular domain ensemble, or that (b) all of the domains were fundamentally exclusive. Thus, the correct way to assess G is to consider significant positive results as a rejection of the null hypothesis that the participant lacks generalizing intelligence. Due to it being derived from the CE matrix, the larger the ensemble of domains, the more informative it becomes.
It must be reiterated that a negative G result does not mean that the participant lacks generalizing intelligence, even if the domains chosen for the ensemble are known to be mutual. It is entirely up to the implementation of the participant, which may be better at generalizing some domains over others. This is a difficult notion, and is often incorrectly assumed to be part of strong artificial intelligence by default. Recall from the chapter on Machine Consciousness that generalizing capacity can be highly variable across implementations.
The mathematical definition for general intelligence (G) follows:
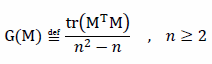
Where M is the CE matrix for the participant, and n is the number of domains in the ensemble, i.e., the dimension of the CE matrix, which must be square with a zero diagonal. The denominator portion of the definition accounts for the fact that the diagonal is zero, and that there is zero CE between a domain and itself. The numerator portion of the definition is the scalar product of the CE matrix with its transpose. This removes signs on the reflected values, as any sensitivity to domains is representative of generalizing capacity. As a result, G is never negative. Alternatively, one could acquire a more linear measure that has more sensitivity to sparse CE matrices by replacing the numerator operations with the element-wise grand sum of the absolute values of the CE matrix. The resulting G is comparable between participants within the same ensemble used to construct the CE matrices between them. It can still be used between participants where the domain ensembles differ, but may be less informative, as negative results do not necessarily indicate a lack of ability.
It is predicted here that all narrow forms of artificial intelligence, including deep learning, and all current machine learning approaches, will exhibit zero G.
Of note is that mutual domains also have an intrinsic cap on conditional effectiveness. It was mentioned previously that a zero CE does not indicate that there is not mutual dependency between domains, but rather, that the implementation failed to indicate one. This is nuanced further by understanding that a bound exists between mutual domains that does not necessarily allow a CE to reach its maximum. What this means is that two domains may be perfectly mutual, but that the best theoretical possible CE between them would be less than 1. These caps are unknowable, and, in turn, have an impact on G, in that even a perfect intelligence would be incapable of achieving maximum CE in all domains due to the inherent structural dependency between them. This is why the maximum G of 1 is not attainable in practice. It is more informative as a comparative measure, where results can be normalized relative to a set of participants or used between different versions of the same participant.
6.6 Future Considerations
This concludes the treatment of the tests and measures of general intelligence. Future considerations include investigations into computational epistemology, and the mapping out of the hierarchy induced by the conditional effectiveness between domains.
Further extensions to EI, CE, and G include the application of G to comparisons over time, integrating into discrete time steps to look for how G response changes as the system makes progress.
An investigation needs to take place on the requisite domain ensemble (RDE) concept. What domains are the most important to protecting the integrity of the systems? These technical considerations presuppose moral intelligence just as one’s knowledge presupposes the ability to make decisions, even on values which are in agreement with what is desired. The RDE is thus paramount. Several common sense candidates are clear, but getting them into a format that is best for a strong AI implementation is a separate challenge.
Verification of knowledge is also going to be another challenge related to anti-effectiveness, in that no matter what is learned, it must remain true to its likeness. This is another reason why obfuscated learning methods based on weighted graphs and deep numerical skeins are undesirable; transparent learning systems are going to be essential to security.
These measures also enhance self-modifying systems, as they could be used as a means for model selection. This is perhaps the most exciting application of these results, as it gives the ability to objectively evaluate the learning performance of cognitive architectures.
Ultimately, however, the goal is to construct working AI implementations that exhibit generalizing intelligence. With these tests, we now have the ability to fully investigate this direction of research. The next step is to begin developing the algorithms and architectures that can exploit the inherent structure between knowledge domains. If the theories in this book are true, then this will call for the creation of sentient processes, with entirely new machine learning approaches that are based on experiential processing.
References
J. Hernández-Orallo, “A (hopefully) non-biased universal environment class for measuring intelligence of biological and artificial systems,” in Artificial General Intelligence, 3rd Intl Conf, 2010, pp. 182–183.
B. Goertzel, “Toward a formal characterization of real-world general intelligence,” in Proceedings of the 3rd Conference on Artificial General Intelligence, AGI, 2010, pp. 19–24.
J. Insa-Cabrera, D. L. Dowe, S. Espana-Cubillo, M. V. Hernández-Lloreda, and J. Hernández-Orallo, “Comparing humans and AI agents,” in Artificial General Intelligence, Springer, 2011, pp. 122–132.
J. Insa-Cabrera, D. L. Dowe, and J. Hernández-Orallo, “Evaluating a reinforcement learning algorithm with a general intelligence test,” in Advances in Artificial Intelligence, Springer, 2011, pp. 1–11.
C. Hewitt, P. Bishop, and R. Steiger, “A universal modular actor formalism for artificial intelligence,” in Proceedings of the 3rd international joint conference on Artificial intelligence, 1973, pp. 235–245.
M. Hutter, “Universal algorithmic intelligence: A mathematical top→ down approach,” in Artificial general intelligence, Springer, 2007, pp. 227–290.
S. Legg and J. Veness, “An approximation of the universal intelligence measure,” arXiv preprint arXiv:1109.5951, 2011.
J. Hernández-Orallo and D. L. Dowe, “Measuring universal intelligence: Towards an anytime intelligence test,” Artificial Intelligence, vol. 174, no. 18, pp. 1508–1539, 2010.
S. Legg and M. Hutter, “Universal intelligence: A definition of machine intelligence,” Minds and Machines, vol. 17, no. 4, pp. 391–444, 2007.
M. Hutter, “Towards a universal theory of artificial intelligence based on algorithmic probability and sequential decisions,” in Machine Learning: ECML 2001, Springer, 2001, pp. 226–238.
N. Bostrom, “Ethical issues in advanced artificial intelligence,” Science Fiction and Philosophy: From Time Travel to Superintelligence, pp. 277–284, 2003.
E. Yudkowsky, “Intelligence Explosion Microeconomics,” Citeseer, 2013.
N. Bostrom, “Hail Mary, Value Porosity, and Utility Diversification,” 2014.
M. Blaze, W. Diffie, R. L. Rivest, B. Schneier, and T. Shimomura, “Minimal key lengths for symmetric ciphers to provide adequate commercial security. A Report by an Ad Hoc Group of Cryptographers and Computer Scientists,” DTIC Document, 1996.
J. O. Pliam, “On the incomparability of entropy and marginal guesswork in brute-force attacks,” in Progress in Cryptology—INDOCRYPT 2000, Springer, 2000, pp. 67–79.
D. J. Bernstein, “Understanding brute force,” in Workshop Record of ECRYPT STVL Workshop on Symmetric Key Encryption, eSTREAM report, 2005, vol. 36, p. 2005.
D. B. West and others, Introduction to graph theory, vol. 2. Prentice hall Upper Saddle River, 2001.
J. Devillers and A. T. Balaban, Topological indices and related descriptors in QSAR and QSPAR. CRC Press, 2000.
S. Pemmaraju and S. Skiena, Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica®. Cambridge university press, 2003.
E. L. Gettier, “Is justified true belief knowledge?,” analysis, pp. 121–123, 1963.
R. Nozick, Philosophical explanations. Harvard University Press, 1981.
M. Swain, “Epistemic defeasibility,” American Philosophical Quarterly, pp. 15–25, 1974.
M. Steup, “Knowledge and skepticism,” 2005.
P. Markie, “Rationalism vs. empiricism,” 2004.
M. Polanyi, “Knowing and being: Essays,” 1969.
W. P. Alston, Beyond“ justification”: Dimensions of epistemic evaluation. Cambridge Univ Press, 2005.
M. Devitt, Realism and truth, vol. 296. Cambridge Univ Press, 1984.
W. P. Alston, A realist conception of truth. Cambridge Univ Press, 1996.
L. Daston, “Objectivity,” 2007.
D. Davidson, “Truth and interpretation,” Claredon, New York, 1984.
J. J. Morrone and J. V. Crisci, “Historical biogeography: introduction to methods,” Annual review of ecology and systematics, pp. 373–401, 1995.
K. T. Kelly, “The logic of success,” Philosophy of science today, pp. 11–38, 2000.
K. T. Kelly, Naturalism Logicized. Springer, 2000.
K. Kelly, “Learning theory and epistemology,” in Handbook of epistemology, Springer, 2004, pp. 183–203.
K. T. Kelly and O. Schulte, “The computable testability of theories making uncomputable predictions,” Erkenntnis, vol. 43, no. 1, pp. 29–66, 1995.
K. T. Kelly, O. Schulte, and C. Juhl, “Learning theory and the philosophy of science,” Philosophy of Science, pp. 245–267, 1997.
N. Rugai, Computational Epistemology: From Reality to Wisdom. Lulu. com, 2012.
O. Schulte and C. Juhl, “Topology as epistemology,” The Monist, pp. 141–147, 1996.
R. Parikh, L. S. Moss, and C. Steinsvold, “Topology and epistemic logic,” in Handbook of spatial logics, Springer, 2007, pp. 299–341.
W. Sieg, “Calculations by man and machine: conceptual analysis,” 2000.
A. R. Jensen, “The g factor: The science of mental ability,” 1998.
D. E. Knuth, “Big omicron and big omega and big theta,” ACM Sigact News, vol. 8, no. 2, pp. 18–24, 1976.

